Comprehensive Guide to the Top Clustering Methods for Omics Data Analysis

In transcriptomics, metabolomics, and single-cell multi-omics studies, clustering analysis serves as a fundamental technique for uncovering underlying patterns within complex biological data. As a key method in unsupervised learning, clustering analysis allows for the grouping of samples or variables based on their intrinsic similarities, without the need for predefined labels (such as "resistant vs. susceptible"). This capability enables researchers to explore natural structures within the data and provides valuable insights for subsequent biological interpretations. This article offers a comprehensive overview of clustering analysis, covering its core concepts, popular algorithms, selection criteria, evaluation methods, and real-world applications, empowering you to apply omics clustering techniques with expertise.

Why Clustering Is Essential for Omics Data Analysis

One of the primary challenges in omics research is the "dimension reduction and interpretation of high-dimensional data." For instance, the spatial single-cell data of tomato callus includes 28,036 individual cells and 19,821 genes, making direct analysis highly complex. In bioinformatics, clustering simplifies such vast datasets into meaningful, interpretable modules by grouping data points based on their similarity.

• Sample Clustering: Unsupervised clustering can categorize these cells into seven distinct groups, enabling the precise annotation of key cell types, such as epidermis, vascular bundles, and meristematic cells. Moreover, clustering reveals that meristematic cells are predominantly located near the epidermis, providing important biological insights.
• Variable Clustering: Simultaneously, genes can be grouped based on their expression profiles, identifying gene modules associated with specific functions. For example, clustering may identify a photosynthetic gene module that is highly expressed in the green tissue cells surrounding the meristem, suggesting a potential role in photosynthesis.

What Is Clustering Analysis in Omics Research?

Core Definitions of Clustering Analysis

Clustering analysis is a fundamental unsupervised learning method that groups data into multiple "clusters" based on the similarity between samples or variables. In this process, objects within the same cluster are highly similar to each other, while those in different clusters exhibit less similarity. In omics research, the "objects" being clustered can refer to samples (e.g., plants, cells) or variables (e.g., genes, metabolites). Unlike supervised learning techniques (such as Partial Least Squares Discriminant Analysis or PLS-DA), clustering analysis does not require a "prior hypothesis." Even when the true categories of the samples are unknown, clustering allows for the discovery of the inherent structure within the data, providing valuable insights without the need for predefined labels.

The Key Role of Clustering in Interpreting Omics Data

Improving Data Analysis Efficiency: 

Omics research often involves large and complex datasets. Clustering helps by quickly filtering out key features and simplifying high-dimensional data, making it easier to manage and analyze. For instance, in proteomics, clustering analysis can identify groups of differentially expressed proteins, which can be pivotal for the rapid identification of disease-related signaling pathways, thus accelerating the discovery of biomarkers.

Optimizing Sample Classification and Revealing Intrinsic Data Structures: 

Clustering analysis is instrumental in classifying samples based on intrinsic data patterns, such as gene expression or metabolite content. By grouping similar data points together, clustering reveals the underlying structure of the dataset. In single-cell transcriptomics, for example, clustering can help classify a heterogeneous cell population into distinct subtypes (such as immune cells or epithelial cells). In plant stress experiments, clustering can differentiate between "tolerant" and "sensitive" subgroups, providing insights into the biological response to stress.

Discovering Potential Biomarkers: 

Clustering analysis can also be used to identify gene clusters with similar expression patterns across large omics datasets. These clusters often correspond to specific biological functions or pathways. For example, clustering analysis could uncover gene clusters whose expression levels continuously rise with prolonged cold treatment, helping to pinpoint genes potentially involved in cold resistance and offering valuable targets for further research.

Common Clustering Algorithms in Omics

Omics data typically consists of high-dimensional datasets, such as those found in single-cell transcriptomics, where thousands of genes are analyzed across diverse sample types (e.g., different plant varieties or treatment conditions). As a result, the choice of clustering algorithm can vary significantly depending on the dataset. Below are three of the most commonly used clustering algorithms in omics and their respective applications:

1. Hierarchical Clustering

Hierarchical clustering is a widely-used algorithm in omics research, particularly suited for gene expression data such as RNA-seq differential gene analysis. It constructs a dendrogram (tree diagram) by either agglomerative (bottom-up) or divisive (top-down) methods, visually displaying the hierarchical relationships between samples or features. A key advantage of hierarchical clustering is that it does not require a predefined number of clusters. This flexibility allows the dendrogram to reveal the phylogenetic relationships among samples or the co-expression patterns of genes.

Core Logic & Steps:

• Step 1: Calculate similarity using distance metrics, such as the Pearson correlation coefficient or Euclidean distance.
• Step 2: Treat each sample or variable as an independent cluster.
• Step 3: Iteratively merge the two most similar clusters until all objects are grouped into one cluster.
• Step 4: Generate a dendrogram to visualize the clustering process and "prune" the tree at a chosen height to determine the final number of clusters.

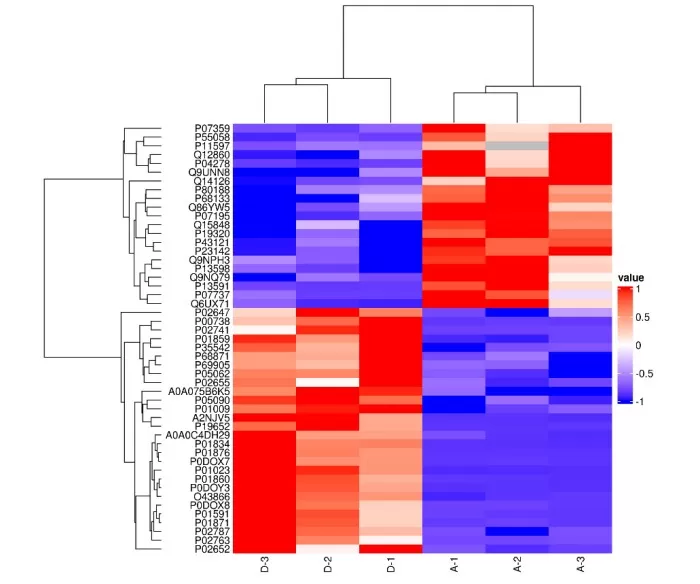
Hierarchical Clustering Heatmap

While hierarchical clustering offers a flexible and visually intuitive approach, it does come with some drawbacks. It is computationally expensive, making it less suitable for datasets with more than 1000 samples. Additionally, the algorithm is sensitive to noise, meaning that outliers can interfere with the clustering process, potentially distorting the results. Despite these limitations, its ability to generate clear visual representations, particularly when combined with heatmaps, makes it a popular choice in omics data analysis.

2. K-Means and Its Variants

K-Means is a highly efficient and scalable clustering algorithm that is particularly effective for handling large datasets. It is well-suited for high-dimensional omics data, where fast computation is crucial. However, one key requirement of the K-Means algorithm is that the number of clusters (K) must be predefined.

Core Logic & Steps:

• Step 1: Predefine the number of clusters (K).
• Step 2: Randomly select K samples as initial cluster centers.
• Step 3: Assign each sample to the nearest cluster center.
• Step 4: Recalculate the center of each cluster and repeat steps 3 and 4 until the cluster centers stabilize.

K-Means Clustering Diagram

K-Means excels in computational efficiency, making it ideal for large datasets with many variables. It allows for quick grouping of samples into clusters based on similarity. However, K-Means has its limitations. Since the number of clusters must be set in advance, this can introduce bias or lead to less optimal cluster assignments if K is chosen incorrectly. Additionally, the results are dependent on the initial cluster center selection, which can sometimes lead to inconsistent outcomes if the initial points are poorly chosen.

3. Hierarchical vs K-Means Clustering in Omics

Both Hierarchical Clustering and K-Means are among the most widely used algorithms in omics research. When choosing between these methods, it’s important to consider the following comparisons:

4. Density-Based Methods (e.g., DBSCAN)

DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is a density-based clustering algorithm that excels in identifying clusters of arbitrary shapes and handling outliers. Rather than grouping data based on distances between points, DBSCAN defines clusters as regions of high data density, which makes it ideal for detecting non-spherical clusters and noise (outliers).

Core Logic for Omics:

• Epsilon (ε): Defines the "neighborhood radius" of each point (e.g., 0.5 in standardized distance).
• MinPts (Minimum Points): Specifies the minimum number of points required within a neighborhood for it to be considered a cluster (e.g., 5).

One of the major strengths of DBSCAN is that it does not require a predefined number of clusters (K). This allows it to adapt more flexibly to the structure of the data. Additionally, DBSCAN automatically filters out outliers, making it particularly useful in datasets where noise is prevalent. However, DBSCAN is sensitive to the choice of two key parameters: Epsilon (ε) and MinPts. Fine-tuning these parameters is essential for obtaining accurate results, and the process can be computationally intensive in large datasets.

Choosing the Right Clustering Method Based on Omics Data Type

The choice of clustering analysis method should be closely tied to core features of the data: data dimensions, sample size, cluster shape, and distribution characteristics. The following is a framework for making the correct selection:

Evaluating Clustering Performance in Omics

To ensure the reliability and accuracy of clustering analysis, it is essential to validate the results using quantitative metrics. This helps avoid false positive clusters—such as random groupings that appear to have meaningful patterns. In omics research, the most commonly used metrics for evaluating clustering quality include the silhouette score (internal validation) and the Rand Index (external validation). These metrics provide a comprehensive assessment of how well the clustering results reflect the true data structure.

Internal Metrics (Evaluation Without Reference Labels)

When reference labels are not available—such as when clustering unknown plant samples—the following internal metrics are commonly used:

• Silhouette Score: This metric measures how similar a sample is to its own cluster compared to other clusters. The score ranges from -1 to +1, with values closer to +1 indicating better clustering. For example, in plant single-cell clustering, a higher silhouette score generally signifies more reliable clustering with clearer cell type classification.
• Davies-Bouldin Index (DB Index): The DB Index quantifies clustering quality by calculating the ratio of intra-cluster compactness to inter-cluster separation. A lower DB index indicates better clustering performance, as it reflects well-defined, distinct clusters.

External Metrics (Evaluation With Reference Labels)

When reference labels are available—such as known plant varieties or treatment groups—the following external metrics are used to assess clustering performance:

• Rand Index: This metric measures the agreement between the clustering results and true labels, such as "stressed group" versus "control group." The Rand Index ranges from 0 to 1, with values closer to 1 indicating greater consistency with the true labels.
• F1 Score: The F1 score balances precision (the proportion of true samples correctly assigned to a cluster) and recall (the proportion of samples in the cluster that were correctly classified). The score ranges from 0 to 1, with values closer to 1 reflecting better clustering performance and a more accurate model.

Conclusion: Making Clustering Work for You

Clustering analysis is a cornerstone tool in omics data research, enabling the discovery of hidden patterns. However, there is no "one-size-fits-all" algorithm. The key to choosing the right method lies in aligning the algorithm with the specific features of the data and the objectives of the research. Below are recommendations for selecting the appropriate clustering method based on different scenarios:

Small Sample Size and Need for Heatmap Visualization

In this case, Hierarchical Clustering is the preferred method. Hierarchical clustering generates a dendrogram (tree diagram), which can be directly linked with gene expression heatmaps to visually display the clustering relationships among samples or genes. This approach is especially useful for illustrating co-expression modules of differential genes and the hierarchical structure of sample subtypes.

Large Sample Size and Spherical Clusters

For large datasets with approximately spherical clusters, K-Means++ is ideal. K-Means has a time complexity of O(nk) (where k is the number of iterations), making it well-suited for large sample sizes. K-Means++ improves upon the classic K-Means algorithm by selecting initial cluster centers based on distance weighting, reducing the impact of random bias and enhancing stability.

Non-Spherical Clusters and Presence of Outliers

In cases where clusters are non-spherical or contain outliers, DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is recommended. DBSCAN defines clusters based on density connectivity, which allows it to identify clusters of arbitrary shapes. It does not require the number of clusters to be predefined and inherently labels noise points (outliers) that do not meet the density criteria.

Evaluating Clustering Results

When evaluating clustering performance, it’s essential to use reliable metrics. If no reference labels are available, the Silhouette Score is a useful metric for unsupervised clustering. It measures both the compactness of clusters (similarity within the cluster) and the separation between clusters (dissimilarity between clusters). A higher silhouette score (closer to +1) indicates more reliable clustering, with values typically greater than 0.5 indicating high-quality clustering. In cases where reference labels are available (such as known cell types or disease subtypes), the Adjusted Rand Index (ARI) is the preferred metric for supervised clustering. The ARI compares the clustering results with the true labels, and higher values (approaching 1) suggest that the clustering accurately reflects the true data structure.

Read more

• Metabolomics Batch Effects
• Understanding WGCNA Analysis in Publications
• Deciphering PCA: Unveiling Multivariate Insights in Omics Data Analysis
• Metabolomic Analyses: Comparison of PCA, PLS-DA and OPLS-DA
• WGCNA Explained: Everything You Need to Know
• Harnessing the Power of WGCNA Analysis in Multi-Omics Data
• Beginner for KEGG Pathway Analysis: The Complete Guide
• GSEA Enrichment Analysis: A Quick Guide to Understanding and Applying Gene Set Enrichment Analysis
• Comparative Analysis of Venn Diagrams and UpSetR in Omics Data Visualization