Data Analysis in Metabolomics Biomarker Research

1. Unlocking Biomarkers: A Guide to Vital Health Indicators

2. Metabolomics and Biomarkers: Unveiling the Secrets of Biological Signatures

3. Choosing the Right Study Design for Metabolomics Biomarker Discover

4. Metabolomics Biomarker Screening Process

5. Identifying the Right Samples: A Guide to Metabolomics Biomarker Research

6. Data Normalization in Metabolomics Biomarker Research

7. Data Cleaning in Metabolomics Biomarker Research

Welcome back to our ongoing journey through the intricate landscape of metabolomics biomarker research. Metabolomics research generates a large amount of data, which have complex characteristics such as high dimensionality and high noise. How to extract valuable information from complex metabolomics data and screen out potential biomarkers has become a hotspot and difficulty in metabolomics research in recent years. In our previous discussions, we meticulously outlined the pivotal steps involved in data preprocessing, encompassing everything from data normalization and outlier management to addressing missing values and batch correction. These preparatory measures are fundamental in ensuring the reliability and accuracy of our dataset, laying the groundwork for insightful analysis.

As we transition into the realm of data analysis, we are poised to unlock the potential of our metabolomics data to reveal crucial insights into health and disease. Over the upcoming blogs, we will delve into a series of advanced analytical techniques tailored specifically for metabolomics research. Each technique plays a vital role in extracting valuable information from our dataset. In this first installment, we will introduce metabolites overall analysis, providing a comprehensive overview of how this approach illuminates the intricate interplay of metabolites within biological systems. Subsequent blogs will delve deeper into specific aspects of data analysis, including screening for differential metabolites, biomarker screening, biomarker performance characterization, and analysis of metabolite functions.

1. PCA

The principal component analysis (PCA) is a multidimensional data statistical analysis method with unsupervised pattern recognition.

1.1 Principle of PCA

As metabolomics data are characterized by “high dimensionality, high noise, and high variability”, multivariate statistical analysis is generally used to “simplify and downsize” the high-dimensional and complex data while retaining the original information to the greatest extent possible and to establish a reliable mathematical model to summarize the metabolic profiles of the research subjects. Principal component analysis (PCA) is an unsupervised pattern recognition method for statistical analysis of multidimensional data, which converts a set of potentially correlated variables into a set of linearly uncorrelated variables by orthogonal transformation. The converted set of variables is called principal components. A simple understanding of the data processing principle of PCA is that the raw data is compressed into n principal components to characterize the original dataset, with PC1 representing the most distinctive feature that describes the multidimensional data matrix, PC2 representing the most distinctive feature that describes the data matrix other than PC1, and PC3 ......PCn and so on.

This analysis is often used to study how to reveal the internal structure among multiple variables through a few principal components, i.e., to derive a few principal components from the original variables so that they retain as much information as possible about the original variables and are uncorrelated with each other. The usual mathematical processing is to make a linear combination of the original multiple indicators as a new composite indicator (Erikssonet et al., 2006).

1.2 The usefulness of PCA

Principal component analysis of the samples provides a preliminary understanding of the overall metabolite differences between groups of samples and the magnitude of variability between samples within groups. In addition to being used to screen for outliers, as mentioned in the previous section, PCA can also be used for quality control and to visualize between-group differences.

a. Quality control

Quality control (QC) samples are prepared by mixing sample extracts and are used to analyze the reproducibility of samples under the same treatment. During instrumental analysis, one QC sample is typically inserted in every 10 samples detected to monitor the reproducibility of the analytical process. The QC samples are complete technical duplicate feeds and, therefore, should be in close proximity to each other and shown as clustered together on the PCA plot.

b. Intuitively reflecting differences between groups

PCA is an unsupervised statistical analysis of data, making it capable of restoring the truest metabolic state within a sample. If there is a clear trend of separation between two groups of samples in the PCA score plot, it suggests that there is a significant difference in the metabolite composition of these two groups of samples.

In addition, PCA can also reflect the variation trend of metabolite composition among samples when analyzing three or more groups of samples, e.g., in a drug treatment study, when the treatment group is clustered with the control group and the model group by PCA, the treatment group will be in between the rest two groups in terms of PC1, which indicates that the treatment has exerted a certain effect and restored the metabolite composition of samples toward the normal control group.

1.3 PCA results interpretation

The most common aspect of PCA analysis results is the score plot. The PCA score plot is available in two-dimensional and three-dimensional display forms. In a two-dimensional score plot, the horizontal coordinate PC1 denotes the first principal component, the vertical coordinate PC2 denotes the second principal component, the percentage denotes the proportion of the explained dataset by this principal component, and the circle denotes the 95% confidence interval. Each dot in the plot denotes a sample, and samples in the same group are represented by the same color. The "Group" shows different groups. In a three-dimensional score plot, a third principal component is added, in which case the X-axis denotes PC1, the Y-axis denotes PC3, and the Z-axis denotes PC2.

The PCA score plot allows us to visualize the similarity between the samples. For example, if several sample dots are clustered together in a PCA score plot, it means that the similarity between these samples is very high. Conversely, if several sample dots are very dispersed, it means that the similarity between these samples is relatively low.

In addition to the score plot, we may also see line plots such as the one below in the results file, which depicts the proportion of the explained dataset by the first 5 principal components. The horizontal coordinates represent the individual principal components, and the vertical coordinates represent the percentage of the explained dataset by the principal component. The left panel shows the cumulative explained proportion; the right panel shows the explained proportion by each principal component.

2. OPLS-DA

One of the common multivariate statistical analysis methods besides PCA is OPLS-DA. OPLS-DA, known as Orthogonal Partial Least Squares-Discriminant Analysis, combines the orthogonal signal correction (OSC) and the PLS-DA method, which is able to decompose the X matrix into two types of information (i.e., Y-related and Y-unrelated), and screen for differential variables by removing the irrelevant variances.

2.1 Principle of OPLS- DA

OPLS-DA differs from PCA in that it is a statistical method for supervised discriminant analysis. Partial least squares-discriminant regression is used to model the relationship between metabolite expression and sample category to predict sample category. OPLS-DA requires two files - the sample variable matrix and the sample categorization matrix - to establish sample relationships, as shown below:

X matrix, sample-variable matrix

Y matrix, sample-categorization matrix

In OPLS-DA modeling, the X matrix information is decomposed into two types of information - Y-related and Y-unrelated, where the information of Y-related variables constitutes the predictive principal component and the information of Y-unrelated variables constitutes the orthogonal principal component. Metabolomics data are analyzed based on the OPLS-DA model, and scores for each group are plotted to further demonstrate the differences between the groups (Thévenotet al., 2015).

2.2 The usefulness of OPLS- DA

Natural clustering trends between samples can be observed using the PCA model. However, there may not always be significant differences between samples in different groups, especially for clinical samples where there are many influencing factors, such as gender, age, BMI, geography, diet, and living environment. These factors can bring a lot of noise signals to the metabolomics dataset that are not related to the group information. OPLS-DA is able to separate predefined information unrelated to the grouping from the original matrix to the maximum extent so as to concentrate the most relevant factors to the first principal component. It then searches for the direction of the orthogonal corrective axis of this principal component, which leads to better separation of samples between the groups, weakening the intra-group differences and maximizing the inter-group differences. It is more applicable to the separation of the two groups of samples. It can also predict the grouping of samples, which PCA cannot do.

2.3 Interpretation of OPLS-DA analysis results

The most commonly used plot in OPLS-DA results is the OPLS-DA score plot, in which the horizontal coordinate indicates the predicted principal component, so the horizontal direction shows the inter-group disparity; the vertical coordinate indicates the orthogonal principal component, so the vertical direction shows the intra-group disparity; and the percentage indicates the explained proportion of the dataset by that component. Each dot in the graph represents one sample and samples from the same group are represented by the same color. The "Group" indicates grouping information.

In addition to the score plots, OPLS-DA also yields S-plots, where the horizontal coordinates indicate the covariance of the principal components with the metabolites, and the vertical coordinates indicate the correlation coefficients of the principal components with the metabolites. The S-plot is generally used to select metabolites that are strongly correlated with the main components of the OSC process. Meanwhile, it can also select metabolites that are strongly correlated with Y. The closer to the two corners, the higher the significance of the metabolite. Red dots in the S-plot indicate that the VIP values of these metabolites are greater than or equal to 1, and green dots indicate that the VIP values of these metabolites are less than or equal to 1.

2.4 Model validation of OPLS-DA

Not all data are suitable for analysis using the OPLS-DA model. Therefore, we need to evaluate the model quality through model validation after the model has been established. The parameters of an OPLS-DA evaluation model include R2X, R2Y, and Q2, where R2X and R2Y indicate the proportion of explained X and Y matrices, respectively, by the built model, and Q2 indicates the predictive ability of the model. The closer the three indexes are to 1 indicates that the model is more stable and reliable. The model is considered valid when Q2 > 0.5 and excellent when Q2 > 0.9.

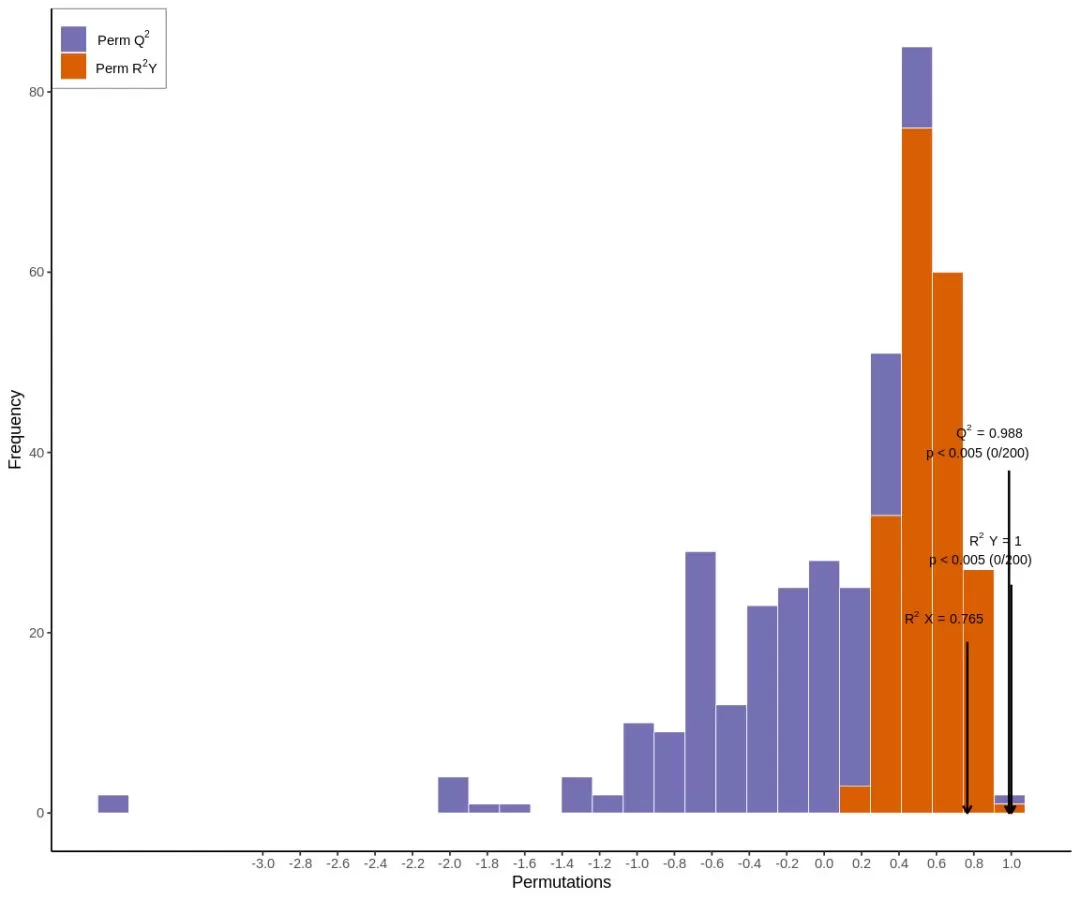
The above chart is the validation plot of an OPLS-DA model, in which the horizontal coordinates indicate the R2Y and Q2 values of the model, and the vertical coordinates are the frequencies at which the model's classification effects emerge, i.e., the present model conducted 200 random permutation experiments on the data, and if p= 0.02 for Q2, it means that there are a total of 4 randomly grouped models with better predictive ability than the present OPLS-DA model in this permutation detection; if p= 0.545 for R2Y, it means that there are 109 randomly grouped models that explain the Y matrix better than the present OPLS-DA model in this permutation detection. In general, the model is optimal when p< 0.05.

3. Cluster analysis

3.1 The principle of cluster analysis

Cluster analysis is a categorical multivariate statistical analysis method. It categorizes individuals, objects, or subjects according to their characteristics so that individuals within the same category have the highest possible homogeneity while the categories have the highest possible heterogeneity.

3.2 The usefulness of cluster analysis

a. Data quality control

The following plot clusters the column data. By looking at the upper dendrogram and the distinction between color legends, it can be noted that the group B samples in orange and the group D samples in rosy red are not clustered together with their respective biological replicates but rather clustered dispersedly across different groups of samples. In particular, two samples from group D clustered with samples in group B, and one sample clustered with samples in group A. This reflects two problems: the first is that the difference between the Group D samples and the Group B samples and Group A samples is relatively small, so there is no clear distinction when clustering is carried out; the second is that Group D samples have poor biological reproducibility, resulting in large variations in group D samples. In this case, we can incorporate PCA data and the sample correlation plot for analysis so as to reflect the real situation of group D samples.

b. It visualizes the variation in differences in the key research objects.

Another function of the heatmap is to visualize the content difference changes of the key research objects. There are thousands of metabolites detected in a single experiment. If all the data from all the samples are presented, it is often not possible to visualize the real variations from one sample to another. We can then display the differential metabolites between the two groups in a clustering heatmap. As shown in the figure below, by displaying the clustered heatmap of the differential metabolites, we can clearly see that the upper part metabolites of group A samples are more abundant than group C samples, and the lower part metabolites are less abundant than group C.

3.3 Interpretation of cluster analysis results

In the heatmap, each row represents a metabolite, and each column represents a sample. The color of each cell in the heatmap shows the content of the metabolite in the row corresponding to the sample in the column. The color changes from red to green based on the level of content, with redder colors indicating higher levels and greener colors indicating lower levels.

We can cluster the column data in the heatmap, where the data clustered together represents that these samples have a relatively consistent expression trend for all metabolites, and these samples are relatively well correlated. In the case of a group of samples with different biological replicates, it means that these biological replicates are relatively consistent. Row data can also be clustered, with clustered metabolites representing a relatively consistent trend of changes in these substances across all samples.