PCoA vs. NMDS in Omics: Choosing the Appropriate Ordination Method

Transforming high-dimensional omics data into intuitive visual representations is a common challenge, particularly in microbiome and metabolomics studies, where the primary interest often lies in sample-to-sample dissimilarity rather than individual features. Principal Coordinates Analysis (PCoA) and Non-metric Multidimensional Scaling (NMDS) are two widely used ordination methods for this purpose. Although both generate two- or three-dimensional scatter plots to summarize similarities or differences among samples, they rely on distinct assumptions and require different interpretative frameworks. This report provides a practical comparison of PCoA and NMDS, outlines common methodological considerations, and proposes a simple decision framework to guide method selection in omics studies.

Quick Takeaway: When to Use PCoA vs NMDS

PCoA is recommended when a fast and stable ordination is needed, with axes that directly summarize the distance structure and can be easily reported.

NMDS is more suitable for complex or strongly non-linear data, particularly when preserving the rank order of dissimilarities is more important than maintaining exact distances.

In practice, both methods are often applied in parallel: PCoA for initial exploration and NMDS as a robustness check, especially in noisy ecological or community-level datasets.

PCoA Explained: What It Preserves and What Axes Mean

Principal Coordinates Analysis is a distance-based dimensionality reduction and visualization technique. It begins with an n × n distance or dissimilarity matrix (e.g., Bray–Curtis or UniFrac) and derives a low-dimensional coordinate system that approximates the original pairwise distances as accurately as possible. The method first computes the distance matrix using an appropriate metric, followed by a centering transformation that converts distances into an inner-product–like matrix. This matrix is then subjected to eigendecomposition, and sample coordinates are obtained from the leading eigenvalues and eigenvectors. The first two or three axes are typically plotted to visualize the dominant patterns of dissimilarity among samples.

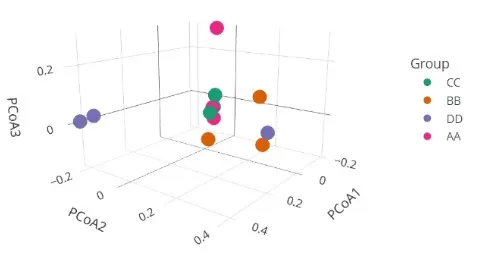
3D PcoA Plot

A major practical advantage of PCoA is that it reports the proportion of total inertia (i.e., distance-based variance) explained by each axis, allowing straightforward assessment and reporting of how much of the overall distance structure is captured in the ordination. learn more at: Principal Coordinates Analysis (PCoA): Principles, Applications, and a Comparison with PCA

NMDS Explained: Rank-Based Ordination for Non-Linear Patterns

Non-metric Multidimensional Scaling is also a distance-based ordination method, but it emphasizes preservation of the rank order of dissimilarities rather than their absolute values. Instead of relying on a single eigendecomposition step, NMDS employs iterative optimization to identify a low-dimensional configuration of points in which inter-point distances exhibit a monotonic relationship with the original dissimilarities. Because NMDS is non-metric and rank-based, it is particularly effective for datasets characterized by non-linear relationships, noise, or outliers, which are common in ecological community analyses and high-dimensional metabolomics data.

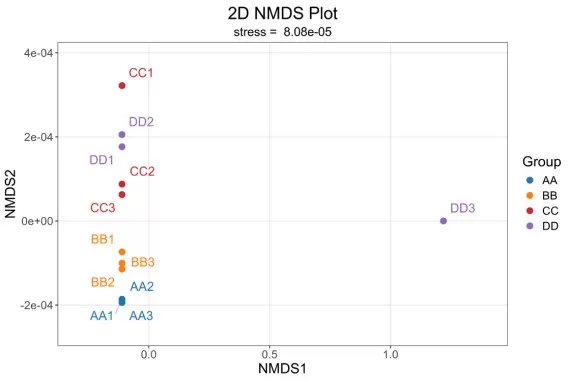
2D NMDS Plot

NMDS Stress: How to Judge Fit

Unlike PCoA, NMDS does not provide variance-explained values for individual axes. Model fit is instead evaluated using the stress statistic, which quantifies the mismatch between distances in the ordination space and the rank structure of the original dissimilarities.

• Stress < 0.10 indicates a good fit
• Stress between 0.10 and 0.20 suggests an acceptable fit that should be interpreted with caution
• Stress > 0.20 indicates a poor fit and potentially unreliable ordination

It is important to note that NMDS solutions may converge to local minima. To ensure robustness and reproducibility, multiple random starts should be performed, and the solution with the lowest stress should be reported.

PCoA vs NMDS: A Comparative Summary

PCoA aims to preserve pairwise distances through a metric embedding and is typically computed via eigendecomposition, making it computationally efficient. Its axes are directly interpretable, as they are associated with the proportion of inertia explained. PCoA is well suited for rapid data exploration and routine β-diversity visualization but may yield negative eigenvalues depending on the distance metric, and two-dimensional representations may capture only a limited fraction of the total structure.

In contrast, NMDS preserves the rank order of dissimilarities using non-metric embedding and relies on iterative optimization, which is computationally more intensive and sensitive to initialization. Its interpretability depends on stress values rather than axis-wise variance, and it is particularly advantageous for detecting non-linear gradients or subtle shifts in noisy datasets. However, high stress values and convergence to local minima remain key limitations.

PCoA vs NMDS Comparison Table 

A Practical Workflow for Omics Studies

First, select a biologically meaningful distance metric, such as Bray–Curtis, UniFrac, or Jaccard. Next, perform PCoA to obtain a rapid and stable overview of the data structure, and record the proportion of inertia explained by the leading axes. If the data exhibit ambiguous patterns or are suspected to contain non-linear structure, perform NMDS with multiple random starts and evaluate the stress value, optionally using a Shepard plot. Statistical testing of group differences should be conducted using PERMANOVA, accompanied by checks for homogeneity of dispersion. Finally, report all key parameters, including distance metrics, data transformations, dimensionality, random seeds or starting configurations, and relevant fit statistics.

Applications of PCoA and NMDS in Omics Research

PCoA operates on sample-by-sample distance matrices, such as those derived from Bray–Curtis or UniFrac metrics, and projects high-dimensional data into low-dimensional space via eigendecomposition. Its ability to quantify the variance explained by each axis makes it particularly useful for interpreting the contribution of major dimensions to overall sample differentiation. For instance, studies of the human gut microbiota have applied UniFrac-based PCoA to reveal significant differences in community structure between healthy individuals and patients with inflammatory bowel disease [1]. Similarly, dietary intervention studies have used PCoA to demonstrate that changes in diet can rapidly and significantly alter gut microbial β-diversity [2]. These findings illustrate the utility of PCoA in capturing both disease-associated variation and short-term environmental effects on microbial communities.

NMDS, by contrast, avoids linear assumptions and identifies optimal sample configurations through iterative optimization. Model fit is assessed using stress values, with stress below 0.1 generally indicating a reliable representation. NMDS is especially well suited for datasets characterized by high noise levels or non-linear gradients. For example, studies investigating gene expression dynamics in natural marine heterotrophic flagellate communities have employed NMDS to show that functional community dynamics are closely associated with growth stages, highlighting its effectiveness in complex ecological contexts [3].

Conclusion: Selecting the Appropriate Method

In microbiome β-diversity analyses, PCoA is commonly applied with Bray–Curtis or UniFrac distances to visualize community-level differences across experimental conditions, such as case–control comparisons, dietary interventions, or temporal studies. In metabolomics, both PCoA and NMDS are widely used after appropriate normalization and scaling, with PCoA favored for its computational efficiency and interpretability, and NMDS preferred when subtle non-linear patterns are anticipated.

Overall, PCoA and NMDS should be viewed as complementary rather than competing methods. PCoA is well suited for rapid, interpretable summaries of distance structure, whereas NMDS provides a more robust alternative for noisy or non-linear data, provided that stress values are acceptable and solutions are stable. Applying both methods and observing consistent patterns across ordinations can substantially increase confidence in the biological relevance of the results.

References

1. Lozupone CA, Knight R. Global patterns in bacterial diversity. Proc Natl Acad Sci U S A. 2007 Jul 3;104(27):11436-40. doi: 10.1073/pnas.0611525104.

2. Wu GD, Chen J, Hoffmann C, Bittinger K, Chen YY, Keilbaugh SA, Bewtra M, Knights D, Walters WA, Knight R, Sinha R, Gilroy E, Gupta K, Baldassano R, Nessel L, Li H, Bushman FD, Lewis JD. Linking long-term dietary patterns with gut microbial enterotypes. Science. 2011 Oct 7;334(6052):105-8. doi: 10.1126/science.1208344.

3. Obiol A, López-Escardó D, Salomaki ED, Wiśniewska MM, Forn I, Sà E, Vaqué D, Kolísko M, Massana R. Gene expression dynamics of natural assemblages of heterotrophic flagellates during bacterivory. Microbiome. 2023 Jun 15;11(1):134. doi: 10.1186/s40168-023-01571-5.

Learn more:

• Metabolomics Batch Effects
• Understanding WGCNA Analysis in Publications
• Deciphering PCA: Unveiling Multivariate Insights in Omics Data Analysis
• Metabolomic Analyses: Comparison of PCA, PLS-DA and OPLS-DA
• WGCNA Explained: Everything You Need to Know
• Harnessing the Power of WGCNA Analysis in Multi-Omics Data
• Beginner for KEGG Pathway Analysis: The Complete Guide
• GSEA Enrichment Analysis: A Quick Guide to Understanding and Applying Gene Set Enrichment Analysis
• Comparative Analysis of Venn Diagrams and UpSetR in Omics Data Visualization