Principal Coordinates Analysis (PCoA): Principles, Applications, and a Comparison with PCA

Principal Coordinates Analysis (PCoA) and Principal Component Analysis (PCA) are foundational dimensionality-reduction methods in omics research, each offering distinct strengths for analyzing complex biological datasets. While PCA is valued for its simplicity in exploring variance structure, PCoA offers greater flexibility by supporting a wide range of distance metrics—an essential feature in microbiome, ecological, and phylogenetic studies.

If your analysis depends on a domain-specific distance—such as Bray–Curtis or UniFrac for microbiome β-diversity—PCoA is usually the more appropriate tool. If you want to interpret variable loadings or explain variance directly in Euclidean space, PCA remains the standard choice. This guide reviews PCoA’s mathematical foundations, key applications, and practical differences from PCA to help researchers choose the most appropriate approach for their data and research questions.

What PCoA Is (and Why It’s Useful)

PCoA (also called metric multidimensional scaling, or metric MDS) converts an n×n distance matrix into coordinates in a lower-dimensional space (typically 2D or 3D). The goal is to preserve the original pairwise distances as well as possible—so points that are “close” under the chosen metric remain close in the ordination plot.

This makes PCoA especially useful when the most meaningful notion of similarity is not simple Euclidean distance in raw feature space—for example, when your data are compositional, sparse, or inherently ecological/phylogenetic.

How PCoA Works

At a high level, PCoA proceeds through these steps:

1) Takes an n×n distance matrix, D (Euclidean or non-Euclidean)

2) Applies Gower’s double-centering

3) Performs an eigendecomposition to obtain the principal coordinates

4) Projects samples onto axes that maximize the retained distance information

The resulting coordinates satisfy ||xi​−xj|| ≈ dij, where dij​ is the original distance between samples i and j.

Choosing a Distance Metric: The Most Important Decision

Because PCoA starts with distances, the distance metric is not a technical detail—it is the analysis. A few practical guidelines:

1) Bray–Curtis: common for abundance/count-like profiles; emphasizes differences in relative composition and is widely used for microbiome β-diversity.

2) Jaccard: focuses on presence/absence (binary) information; useful when detection vs. non-detection is more reliable than abundance.

3) UniFrac (weighted/unweighted): incorporates phylogenetic relationships; often preferred when evolutionary relatedness matters.

4) Euclidean/Manhattan: can be appropriate for normalized continuous measurements, but may be less robust for sparse compositional profiles.

A good practice is to justify the metric in one or two sentences in your methods section: what biological difference does it measure, and why is it appropriate for your data type?

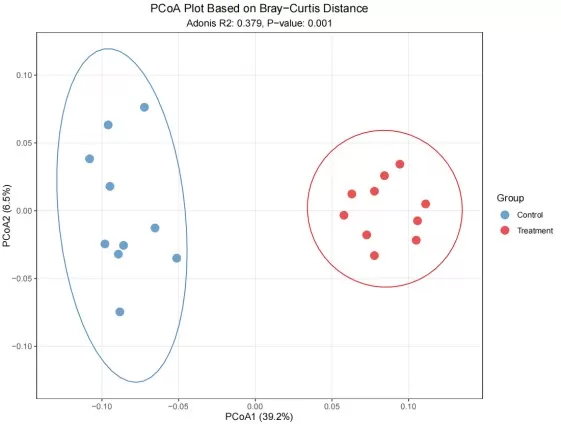
2D PCoA Score Plot with Group Clusters and Contribution

How to Read a PCoA Plot

A typical PCoA plot shows each sample as a point in the ordination space. Interpretation is distance-based:

• Each point represents a sample and is colored by the predefined group.
• Ellipses indicate 95% confidence intervals around the group centroids.
• Clustering indicates similarity in the distance-based ordination space (e.g., Bray–Curtis or UniFrac).
• X-axis: PCoA1 (Principal Coordinate 1)—the percentage indicates the proportion of total inertia in the distance matrix captured by this axis.
• Y-axis: PCoA2 (Principal Coordinate 2)—the percentage indicates the proportion of total inertia in the distance matrix captured by this axis.

Adonis (PERMANOVA) test for group differences

PCoA is often paired with PERMANOVA (the Adonis test), a nonparametric multivariate method based on distance matrices. This approach quantifies how much variation is explained by grouping factors and uses permutation testing to assess the statistical significance of group separation.

Key outputs to report:

• R² represents the proportion of variance explained by the grouping factor; higher R² values indicate stronger explanatory power.
• The p-value (Pr(>F)) is derived from permutation tests; p < 0.05 indicates statistically significant group separation at the 95% confidence level.

Applications of PCoA in Omics

• Microbiome β-diversity analysis—uses ecological distance metrics (e.g., Bray–Curtis and UniFrac) to quantify dissimilarity among microbial communities.
• Ecological community structure—evaluates species–environment relationships using abundance-based distance measures.
• Phylogenetic comparisons—visualize evolutionary divergence patterns using genetic distance matrices.
• Multi-omics integration—supports kernel-based distance measures for cross-dataset alignment.

Advantages of PCoA

• Flexible distance-metric support—accommodates both Euclidean (e.g., Manhattan) and non-Euclidean (e.g., Jaccard) dissimilarities.
• Improved preservation of non-linear relationships—often more robust than PCA for ecological and compositional data.
• Domain-relevant interpretability—well suited to ecological, phylogenetic, and microbiome studies where distance-based inference is central.

PCoA vs. PCA: Key Differences

A simple decision rule: if your scientific question is naturally framed in terms of pairwise dissimilarity (β-diversity, ecological distance, phylogenetic distance), start with PCoA. If you need loadings or want to explain variation directly in the original feature space, start with PCA.

Conclusion: Choosing PCoA vs PCA for Your Data

PCoA is a flexible, distance-first ordination method that shines when Euclidean assumptions are not appropriate or when domain-specific dissimilarity measures carry the biological meaning. Used together with thoughtful metric selection and distance-based tests like PERMANOVA (with dispersion checks), it provides a clear and defensible framework for exploring and reporting group-level patterns in complex omics datasets.

Complete PCoA Analysis Workflow in R

# Application: Microbiome omics data  

# Load required packages

library(vegan)    # Ecological analysis

library(ggplot2)  # Visualization

# 1. Data Preparation (Simulated example data)

set.seed(123)

# Simulate OTU table: 20 samples, 100 species

control_data <- matrix(rpois(10*100, lambda = 10), nrow = 10, ncol = 100)  #（mean~10)

treatment_data <- matrix(rpois(10*100, lambda = 15), nrow = 10, ncol = 100)  #（mean~15)

# Combine data

otu_table <- rbind(control_data, treatment_data)

rownames(otu_table) <- paste0("Sample", 1:20)

colnames(otu_table) <- paste0("OTU", 1:100)

# Group information (10 control vs 10 treatment)

group <- factor(rep(c("Control", "Treatment"), each = 10))

# 2. Calculate Distance Matrix （Bray-Curtis）

dist_bray <- vegdist(otu_table, method = "bray")

# 3. Perform PCoA Analysis

pcoa_result <- cmdscale(dist_bray, k = 3, eig = TRUE)

# Extract main results

scores <- as.data.frame(pcoa_result$points)  # Sample coordinates

colnames(scores) <- c("PCoA1", "PCoA2", "PCoA3")

# Calculate variance explained by each axis

variance <- round(pcoa_result$eig / sum(pcoa_result$eig) * 100, 1)

# 4. Visualization

p <- ggplot(scores, aes(x = PCoA1, y = PCoA2, color = group)) +

    geom_point(size = 4, alpha = 0.8) +

    stat_ellipse(level = 0.95, show.legend = FALSE) + # Add 95% confidence ellipses

    labs(x = paste0("PCoA1 (", variance[1], "%)"),

         y = paste0("PCoA2 (", variance[2], "%)"),

         title = "PCoA Plot Based on Bray-Curtis Distance",

         color = "Group") +

    scale_color_manual(values = c("#377eb8", "#e41a1c"))

# 5. Statistical Testing (Group differences)

adonis_result <- vegan::adonis2(dist_bray ~ group, permutations = 999)

R2 <- round(as.numeric(adonis_result$R2[1]), 3)

pvalue <- signif(adonis_result$`Pr(>F)`[1], 2)

statFlag <- paste0('Adonis R2: ', R2, ', P-value: ', pvalue)

p <- p + labs(subtitle = statFlag)

# 6. Theme Adjustment and Output

p <- p + theme_bw() +

    theme(plot.title = element_text(hjust = 0.5, vjust = 0.5),

        plot.subtitle = element_text(hjust = 0.5, vjust = 0.5),

        panel.grid.minor = element_blank())

png("PCoA.png")

print(p)

dev.off()

Read more:

• Understanding WGCNA Analysis in Publications
• Deciphering PCA: Unveiling Multivariate Insights in Omics Data Analysis
• Metabolomic Analyses: Comparison of PCA, PLS-DA and OPLS-DA
• WGCNA Explained: Everything You Need to Know
• Harnessing the Power of WGCNA Analysis in Multi-Omics Data
• Beginner for KEGG Pathway Analysis: The Complete Guide
• GSEA Enrichment Analysis: A Quick Guide to Understanding and Applying Gene Set Enrichment Analysis
• Comparative Analysis of Venn Diagrams and UpSetR in Omics Data Visualization